A Breakdown | What Is A Real Gas?

What is a Real Gas?

Real gases are non-ideal gases, where two assumptions from the ‘kinetic model’ are not accurate:

• Gas molecules/atoms occupy space,
• Gas molecules/atoms interact with each other.

At high pressures, repulsive forces assist expansion and at intermediate pressures, attractive forces assist compression.

Limit  P = 0, is when the assumptions work (equation 1).

PV = nRT
Equation 1: Ideal gas equation.

(1.1)

To understand the behaviour of real gases, the flowing must be taken into account:

• Vompressibility effects,
• Variable specific heat capacity,
• Van der Waals forces,
• Non-equilibrium thermodynamic effects,
• Issues with molecular dissociation and elementary reactions with variable composition.

The ideal gas approximation can be used with reasonable accuracy, however at certain conditions such as condensation point of gases, near critical points, at very high pressures, to explain the Joule–Thomson effect and in other less usual cases, the real gas model would have to be used, with the deviation from ‘ideal’ conditions being described by a term called the compressibility factor, Z.

Compressibility Factor

The compressibility factor, Z, is the ratio of the measured molar volume of a real gas to the molar volume of an ideal gas at the same temperature and pressure (Equation 2). The compressibility factor is very useful for the modification of ideal gases into real gases, with deviations from ideal becomes more significant the closer the gas is to a phase change or the lower the temperature or larger the pressure.

Molar volume:

V¯=Vn

For an ideal gas:

PV¯ideal=RT

For a real gas:

PV¯real=ZRT

compressibility factor:

Z =V¯realV¯ideal

Equation 2: Compressibility factor equation and the molar volume equations for ideal and real gases.

(1.2)

The compressibility factor generally increases with temperature and pressure, at low pressures Z = 1, which means the gas is ideal. At intermediate pressures Z < 1 and the molecules are free to move to result in attractive forces dominating and a smaller volume. At higher pressures, molecules are colliding more frequently which allows repulsive forces to have a noticeable effect resulting in a higher molar volume making Z > 1. Furthermore, the closer a gas is to its critical point or boiling point, the more Z will deviate from the ideal case (figure 1).

• At low pressures, Z = 1
• At intermediate pressure, Z < 1
• At higher pressures, Z > 1

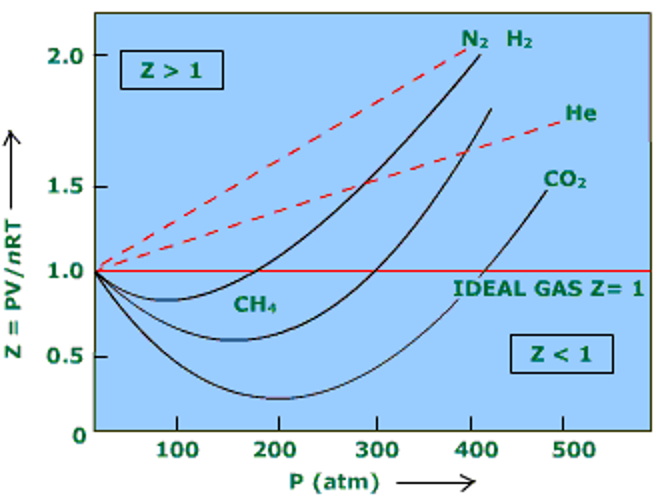
Figure 1: Compressibility Factor Graph (Stack Exchange, 2019).

Notice that, although the curves are approaching the 1 as P = 0 they do so at different slopes.

Principle Of Corresponding States

At different temperatures and pressures, gases will behave differently, but gases will behave similarly to each other at temperatures and pressures normalised concerning their critical temperature (equation 3) and critical pressure (equation4), TC and PC.

TC=TTR

Equation 3: Critical temperature equation.

(1.3)

Pc=PPR

Equation 4: Critical pressure equation.

(1.4)

• Critical Temperature (Tc)
• Critical Pressure (Pc)
• Reduced Temperature (Tr)
• Reduced Pressure (Pr)

The Z factor for all gases is approximately the same at the same reduced temperature and pressure. This is called the principle of corresponding and data can be plotted to form a generalised compressibility chart (figure 2).

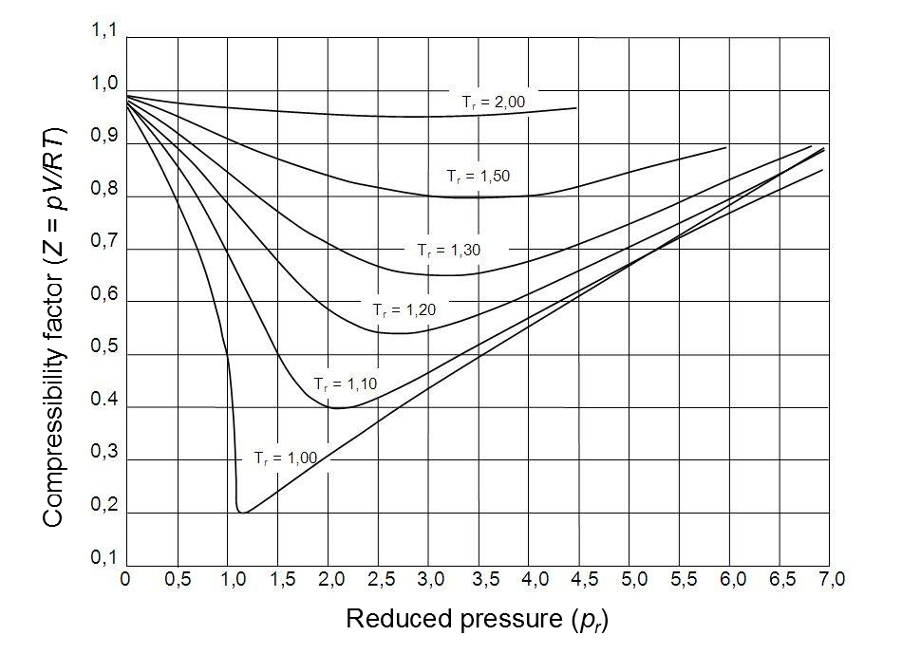
Figure 2: Generalized diagram of compressibility factor (Pugliesi, 2015).

• At low pressures (Pr << 1), gas behave like an ideal gas regardless of the temperature.
• At high temperature (Tr >> 2), ideal gas behaviour is assumed with god accuracy regardless of the pressure.
• The deviation from the ideal gas condition is greatest around the critical point.

All gases have a critical point, with the temperature, pressure and molar volume at the critical point being the critical constant. Above the critical temperature and pressure, gases behave as both liquid and gas (figure 3).

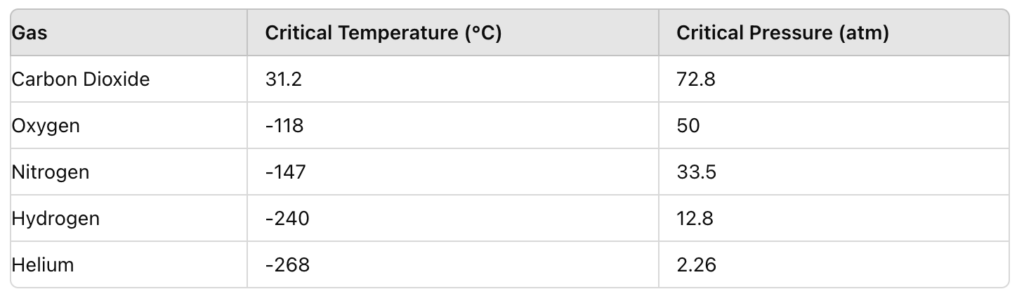
Figure 3: gases and their critical properties (ScienceHQ, 2020).

The Van De Waals Equation

Two parameters are derived from the molecule’s concepts, repulsion and attraction. First, assume the gas molecules are hard spheres to stress the actual volume available for the molecules (equation5):

PV¯=RT ⇒ P(V¯-b)=ZRT

Equation 5: Transformation of the ideal gas equation with the van der Waals ‘b’ term.

(1.5)

For every 1 mole of gas, the real volume for the gas molecules to occupy is the molar volume minus the volume of the sphere, b, with units m3 mol-1 or dm3 mol-1.

The pressure will depend on the frequency and the collision force between gas molecules and the walls of the vessel. The attractive forces between the molecules have strength proportional to the gas concentration (equation 6):

Fattract ∝nV or Fattract ∝1V¯

Equation 6: Equation linking attractive forces and volume/molar volume.

(1.6)

Because the attractive force results in a reduced frequency and force of collisions, the pressure will be reduced in proportion to the square of the concentration, with a and b being the van der Waals coefficients that are independent of the temperature (equation 7).

P=RT(V¯-b) – aV2¯

Equation 7: Van der Waals Equation.

(1.7)

For the van der Waals equation there are two main features:

The first feature is that perfect gas isotherms are obtained at large molar volumes and high temperatures, with the RT term (equation) being too high at high temperatures so the first term greatly exceeds the second term. Also, if the molar volume is too large then the equation (equation) can be reduced to the ideal gas equation (equation).

The second feature is that liquid and gases will co-exist when both the cohesive and dispersing effects are balanced, which is referred to as the van der Waals loop when both terms have the same magnitude, which is very convenient and can predict large errors for some conditions (loops). The first term occurs due to the kinetic energy of the molecules and their repulsive forces, and the second represents the attractive interactions.

References

Pugliesi, D. (2015). File: Compressibility factor generalized diagram.png. Retrieved from Wikimedia Commons: https://commons.wikimedia.org/wiki/File:Compressibility_factor_generalized_diagram.png
ScienceHQ. (2020). Introduction to thermodynamics. Retrieved from ScienceHQ: http://www.sciencehq.com/physics/introduction-to-thermodynamics-2.html
Stack Exchange. (2019). Compressibility Factor Graph – Which gas attains a deeper minimum? Retrieved from Stack Exchange: https://chemistry.stackexchange.com/questions/107843/compressibility-factor-graph-which-gas-attains-a-deeper-minimum