To Read Part 1 for an Introduction, Click here.
Age Related Changes to DNA methylation
Changes in the levels of DNA methylation during ageing have been reported since the1960s. Subsequent studies since then involving different species of mammalians such as rats, mice and human subjects have all shown substantial evidence to support the hypothesis of a progressive loss in levels of DNA methylation during ageing (Singhal RP, 1987; Bollati V, 2009). The expression of the enzymes involved in the process of DNA methylation, DNA methyltransferase (DNMT), have also been reported to change during ageing (Lillycrop, 2013). This is supported by Casillas et al. (2003) who reported that the levels of DNA methyltransferase 1 (DNMT1) and DNA methyltransferase 3a (DNMT3a) declines during the ageing. On the other hand, the levels of DNMT3b increases. The increase in global hypomethylation is supported by these findings as DNMT1 is the maintenance DNMT enzyme (Casillas MA Jr, 2003). Alongside a decrease in global hypomethylation there is also an increase in gene-specific promoter hypermethylation. This is supported by genes that become hypermethylated with age such as the oestrogen receptor (Issa JP, 1994), myogenic differentiation 1 (JP, 2000) and E-cadherin (Kang GH, 2003). Recently Lowe et al 2020. studied DNA methylation “clocks” in naked mole rats as a predictor of ageing. The naked mole rat is the longest-lived rodent (Pappas, 2018). Changes in DNA methylation at 51 CpG sites were analysed from their livers (age 39-144 weeks). Changes in methylation in 23 CpG sites were significantly associated with age. This work supports previous findings that there is a correlation between changes in DNA methylation and increased age in mammals.
Epigenetic drift refers to the errors in maintenance of the epigenome, which is responsible for controlling cell identity and function. This is elegantly summarised by Shah et al. (2014) as the divergence of the epigenome as a function of age due to stochastic changes in methylation (Shah, 2014). This is a hallmark of ageing (Mendelsohn, 2017). To this end Maegawa et al. (2017), measured and analysed the differences between average methylation between three different species: Young mice, Rhesus monkeys and Humans. The study found that the average methylation increased from 2 to 18, 2 to 22 and 3 to 20 within Young mice, Rhesus monkeys and Humans respectively within unmethylated sites compared to the same sites at an older age. It was also found that drift rates were calculated as 4.1%, 0.34% and 0.1% per year for Young mice, Rhesus monkeys and Humans respectively, establishing an inverse relationship between the rate of methylation drift and life expectancy in these species.
Another important age-related factor is the change in expression of DNA methylation and demethylation enzymes. Sun et al. (2014) discovered the expressions for genes encoding for DNMT, DNMT1, DNMT3a and DNMT3b were drastically reduced between the ages of 4 and 24 months within C57BL/6 male mice (Sun, 2014).
DNA methylation changes have been investigated in several longitudinal studies. Feinberg et al. (2010), carried out a genome wide screen over 11 years investigating a sample size of 4 million CpG sites. This produced a result of 227 regions, showing extreme variably methylated regions across the genome, falling into two categories of dynamic and stable methylation (Feinberg AP, 2010). Bjornsson et al. (2008) measured the levels of global DNA methylation in whole blood in two separate investigations. The first was conducted over 11 years and examined whole blood from 111 individuals (59-86 years). The second study was conducted over 16 years and examined whole blood from 127 individuals (5 -72 years). Results revealed 8-10% of individuals studied showed >20% change in methylation over the 11-16-years. Additionally, the changes showed familial clustering of both increased and decreased methylation. Family members did not live in the same household during the study, suggesting genotype influences the rate of change of methylation with age (Bjornsson HT, 2008).
Monozygotic twins have been studied in a bid to discount the effect of genetic background on epigenetic ageing. Fraga et al. (2005) compared the DNA methylation patterns in a pair of 3 year old and 50 year old monozygotic twins and found that the distribution of DNA methylation marks were distinct for the 50 year old monozygotic twins but showed significant overlap of the genomic distribution of the 5-methylcytosine of the 3 year old monozygotic twins (Fraga MF, 2005). A study by Talens et al. (2010) who investigated 460 individuals which comprised 230 monozygotic twin pairs (aged between 18-89 years old). It was found the variation in global DNA methylation increased proportionally with age. This supports the study by Fraga et al. (2005). Mean methylation and variance was also examined for several genes associated with common diseases over a range of candidate ages. Mean methylation did not differ significantly between the young and old ages. Conversely, there was an increase in variation of DNA methylation with age. There was a significant difference in the stability of different CpG sites, the most substantial age related variation increase in DNA methylation appearing at CpG sites linked to metabolic and homeostatic related genes such as IGF-2 and leptin (Talens RP, 2010). DNA methylation from saliva samples of 34 pairs of identical twins (aged between 21-55 years old) was analysed and the results found 88 CpG sites near 80 genes where DNA methylation was substantially correlated with age (Bocklandt S, 2011). Currently it is assumed that one third of the CpG sites reveal age associated DNA methylation changes, of which 60% become hypomethylated and 40% become hypermethylated during ageing (Johansson, 2013). Age associated DNA methylation is related across different tissues. However, it is different depending on the cell type (Teschendorff, 2010).
Epigenetic Clocks
Early studies have eluded to a “clock” underlying ageing (J.Catania, 1991). Conducted in the early 1990’s Catania et al. (1991) suggested that a continuous loss in DNA methylation levels in cell cultures is associated or connected to the number of cell divisions that occur during a cell’s lifetime. Catania et al. (1991), considered that a progressive loss of DNA methylation produces a multi-step cell division “clock” which underlies the Hayflick phenomenon (J.Catania, 1991). According to Hovarth et al. (2013), the epigenetic clock can be described as a prediction method of age based on the linear combination of the DNA methylation levels of 353 CpG dinucleotides (Horvath, 2013). This work provides more evidence that the methylation landscape changes dramatically with ageing.
Biological Versus Chronological Age
Several studies have been conducted to establish whether a participants age’ is biologically different to their chronological age by measuring age acceleration. These studies have either used the Hovarth epigenetic clock which uses 353 CpG dinucleotides or the hannum clock which uses 71 CpG dinucleotides (Fransquet, 2019). Hovarth et al. (2015) found that 55 year olds have a lower DNA methylation age compared to their chronological age and that their offspring have a lower age acceleration and intrinsic age acceleration compared to the controls (Horvath S P. C., 2015). Mcewan et al. (2017) measured Nicoyans from the Nicoya peninsula of Costa Rica where they have one of the highest old age life expectancies in the world. They concluded that there were no age acceleration differences between Nicoyans and age matched controls (McEwen, 2017). Three separate cohorts were analysed and investigated in another study which found DNA methylation age was highly correlated with chronological age (r=0.93). However, they found the correlation was lower in each cohort separately (r= 0.52-0.73) (Armstrong NJ, 2017). Kananen et al. (2016) found that DNA methylation age was moderately correlated with chronological age over the course of 25 years (r=0.54). it also found that younger participants aged faster than older participants (Kananen L, 2016). Epigenetic age predictions do not only correlate with chronological age but are also indicatory for life expectancies (Field AE, 2018).
Mathematical Modelling of DNA Methylation
Mathematical modelling is defined by Southern et al. (2008), as an abstract representation of a complex system in mathematical form (Southern, 2008). Most models used to describe complex biological systems require simplifying assumptions, therefore, the solution of the model becomes an approximation of the original biological system, thus, can be used to provide an understanding into the elements that influence the nature of more complex systems. The accuracy and precision of a model is dependent on the validity of the assumptions, usually the accuracy and precisions of a model are enhanced by making model building an iterative process (Southern, 2008).
Computational modelling has become the cornerstone of biological studies and are routinely conducted alongside laboratory experiments. The computational modelling process essentially involves inputting the mathematics into a computational system to simulate the dynamic behaviour of a biological system under investigation. There are several advantages to computational modelling over traditional approaches. These are:
- a hypothesis can easily be explored by a model,
- a model can be easily updated as the biology of ageing updates,
- experiments can be run quickly and efficiently,
- a model provides a framework for brining disparate biological data together.
Due to its ability to represent the complexities of DNA methylation mathematical modelling has become a tool that has been applied widely in this area. Moreover, due to several factors such as its cost effectiveness, ease of use and efficiency, it overcomes many of the obstacles faced by conventional methods, facilitating the quantitative analysis of complex biochemical systems.
Previous Models of DNA Methylation
One of the first mathematical models of DNA methylation dynamics was developed by Otto et al. (1990) who presented a model for the kinetics of methylation and demethylation of eukaryotic DNA. The model incorporated de novo methylation and an error rate for maintenance methylation. The equation used in the model presented a steady state equilibrium where the rate of newly methylated sites is the same as the rate at which site are demethylated within cell generation. The equations developed by Otto et al. (1990) can be used to analyse the whole genome or specific regions within the genome (Otto, 1990). Kinetic models have also been used to model DNA methylation. An advantage of kinetic modelling. Kinetic models take into account several interlinked enzyme catalysed reaction rates (Sauer, 2010). Unfortunately, a disadvantage of kinetic modelling is they require kinetic parameter data to build them (J. Schaber, 2009). Other approaches have used Markov chains. A Markov chain is defined as a set of transitions, which are determined by a probability distribution which satisfies the Markov property. A Markov property refers to the memoryless property meaning that a given probability distribution is independent of its history (Soni, 2018). An advantage of the Markov model is that it is an analytical method therefore the reliability parameters are calculated using a mathematical formula leading to higher speed and accuracy associated with them (Egerton, 2016). A disadvantage however, is that due to the Markov model being memoryless, if in practice the assumption of memoryless is not completely applicable to the system and how it functions in practice, the accuracy of the model is lessened (Egerton, 2016). Capra et al. (2014) modelled DNA methylation dynamics using approaches from phylogenetics using this approach to combat the lack of models which consider the dependency of precursor and dependant cells. A continuous time Markov chain approach was utilised and tested by the analysis of high-resolution methylation map of mouse stem cells into numerous blood cells, the model achieved a 90% correct score. The model was capable of ascertaining unobserved CpG methylation states from observed methylation states from the same sites in related cell types (Capra, 2014).
Another Markov chain model innovated by Sontag et al. (2006) describes the development of hypo- to hypermethylated equilibria from methylation noise in a fixed number of CpG sites. Sontag et al’s model explains the persistent coexistence of the two equilibria of hypo- and hypermethylated sites, sporadic changes of site-specific methylation levels that may lead to an altering of pre-set epigenetic imprints in renewing cell populations (Sontag, 2006). Przybilla et al. (2014) further expanded on Sontag et al by using a computational approach using the same model of DNA used by Sontag et al (2006) to understand epigenetic changes in ageing within stem cells. Przybilla et al. (2014) combined an individual cell-based model of stem cell populations with a model of epigenetic regulation of transcription enabling a simulation of age related trimethylation of lysine 4 at histone H3 and of DNA methylation. The findings showed that epigenetic ageing intensely affects stem cell heterogeneity and that homing of stem cells niches slows down epigenetic ageing (Przybilla, 2014).
Genereux et al. (2005), developed a probabilistic model of DNA methylation dynamics to better understand how methylated and unmethylated states of Cytosine are transferred during DNA replication. A probabilistic model accounts for randomness, in the form of random variables, which in turn affects model outcomes (Stephanie,2017). This inherent random variable assumption is seen as an advantage. Another advantage is that a probabilistic model often provides a realsiic representation of the biology at a molecular level (S. Bouwman, 2005). A disadvantage is the longer calculation times compared to other modelling techniques (S. Bouwman, 2005). The model was designed to track methylated, hemimethylated and unmethylated CpG/ CpG dyads at a CpG site over several cells from a single tissue within a single individual. The model can infer site-specific rates of de novo methylation and maintenance methylation (Genereux, 2005).
Another probabilistic model representing two kinds of stochasticity was developed by Flottmann et al. (2012). It described the interplay between gene expression, chromatin modifications and DNA methylation. The model deduces cytosine methylation rates at several sites within the Human promoter gene FMR1. However, there were variations in results after extensive analysis showing room for optimization of the process. Faster changes in DNA methylation increasing the speed of the reprogramming at the cost of efficiency whilst enhanced chromatin modifications somewhat improve efficiency (Flöttmann, 2012).
DNA methylation in most tissues and cell lines is stochastically moderately variable with each site reliant on site-specific probabilities (Varley, 2013). A stochastic model is defined as a model which possess randomness embedded within the model (Stephanie, 2016). Riggs and Xiong. (2004) developed a stochastic methylation model in which for each CpG dyad there is a evident efficiency of both maintenance and de novo methylation (Xiong, 2004). Building further on the work done by Riggs and Xiong. (2004), Jeltsch and Jurkowska. (2014) included the rate of cell division in conjunction with active and passive demethylation. This was done by using a stochastic equation model with rates of cell division as well as rates of active and passive demethylation (Jeltsch, 2014). Rannala et al. (2001) utilised a stochastic model to analyse the methylation patterns and stem cell turnovers within the human colon. The findings suggested human crypts are long-lived whilst accumulating random errors in methylation and compromise of stem cells which undergo “bottlenecks” during life. Stem cell bottlenecks are described as events which lead to the drastic reduction of the population size. The remaining population after the bottleneck undergo significant genetic drift (Scitable, population bottleneck, 2014). The stochastic model simulated crypts with a methylation error rate of 2 x 10-5 per CpG site per division, with one division occurring per day (Rannala, 2001). Haerter et al. (2014) used a stochastic simulation of CpG islands. Furthermore, Haerter et al. (2014) found that a dynamic collaboration between CpG’s can provide reliable error tolerant somatic inheritance of both hypermethylated and hypomethylated states of multiple CpGs, this reproduced witnessed, stable bimodal methylation patterns. Inheritance was predicted as being strengthened by the recruitment of demethylating enzymes by unmethylated CpGs, allowing CpG islands to remain hypomethylated within an expanse of hypermethylation (Haerter, 2014). Two years later Olariu et al. (2016) expanded on the work done by Haerter and used the same stochastic model to model the regulatory network of Oct4, Tet1 and Nanog including positive feedback loops comprising of DNA demethylation across the promoters of Oct4 and Tet1. A mechanistic understanding of regulatory dynamics was put forward which outlined that DNA methylation is the key to regulation of pluripotent genes. Most recently, Olariu et al. (2016) provided a template for a novel framework connecting transcription regulation with DNA methylation models (Olariu, 2016).
Partial differential equations were used by McGovern et al. (2012) to produce a dynamic three – compartmental model of DNA methylation based on the activity of DNMT methyltransferase proteins which are as follows: unmethylated CpG dyads, hemimethylated CpG dyads and methylated CpG dyads. These are portrayed in figure 2.1.
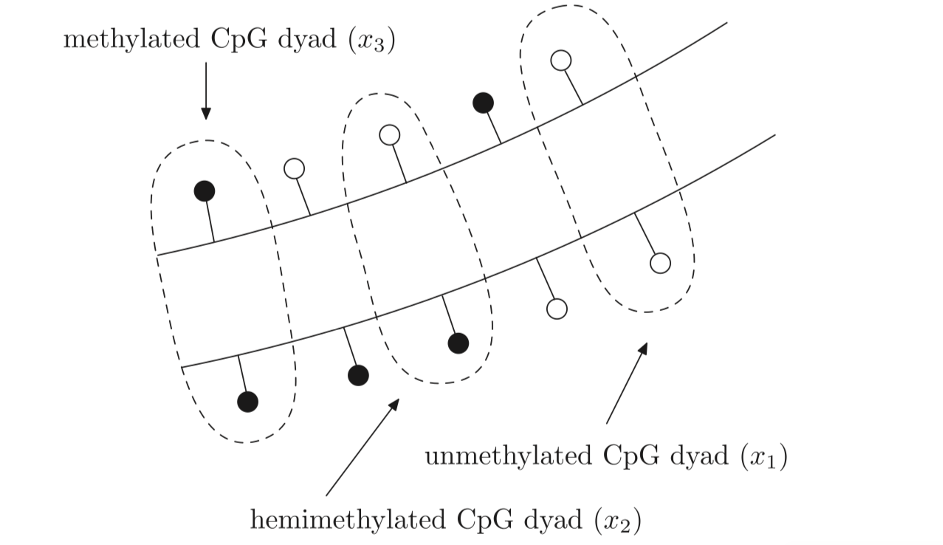
Figure 2.1: Three distinct states of a CpG dyad: unmethylated (x1), hemimethylated (x2) and methylated (x3). An unmethylated CpG site is portrayed as a white circle contrasting to the black circle which depicts a methylated CpG site. An unmethylated CpG dyad has both of the CpG sites opposite one another unmethylated (x1), A hemimethylated CpG dyad has only one of the CpG sites opposite methylated and one unmethylated (x2) and a methylated CpG dyad has both of the CpG sites opposite one another methylated (x3). Figure taken from (Zagkos, 2019).
The model also includes the Tet proteins, which enzymatically transform methycytosine to hydorxymethylcytosine. The DNMT1, DNMT3a and DNMT3b as well as DNA replication are all responsible for the transition states between the CpG dyads. Partial differential equations used in the model as shown in figure 1.2 show the methylation rates of unmethylated and hemimethylated CpG dyads denoted by k1 and k2 respectively. Moreover, the demethylation rates denoted by k3 and k4 represent hemimethylated and methylated CpG dyads respectively. D denotes the rate of cell division see figure 2.2. The model provided an accurate representation of DNA methylation dynamics (McGovern, 2012).
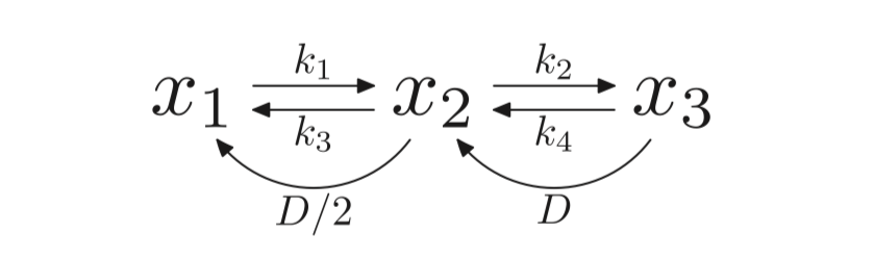
Figure 2.2: A diagram to show the methylation rates between unmethylated (x1), hemimethylated (x2) and unmethylated (x3). Figure taken from (Zagkos, 2019).
In 2013 Zheng et al. (2013) developed a CpGIMethPred, a support vector machine based model which predicts the methylation status of CpG islands within a human genome under normal conditions. The parameters used for prediction within the model are ones that have been previously demonstrated as effective. These included DNA sequence composition patterns, DNA structure patterns, CpG island specific attributes, distribution patterns of conserved transcription factor binding sites and conserved elements and methylation status. The three-part model can be used to gain a CpG island map. This compromises of database extraction of methylation data, feature extraction and statistical predictive modelling (Zheng, 2013). Most recently, a spatial stochastic model has been used by Lück et al. (2020) to model single CpGs and generalize them into multiple CpGs using SAN (stochastic automata network). The results of this model were verified against extensive results from Monte Carlo simulations (Wolf, 2020).
In 2019 Zagkos et al. (2019) developed upon the model created by McGovern et al. (2012).
Summary Table
| Authors | Title | Models Feature/ Predictions and Computational methods used | Evaluation |
| Otto et al (1990) | DNA methylation in eukaryotes: kinetics of demethylation and de novo methylation during the life cycle. | A kinetic model used to produce methylation and demethylation whilst assimilating de novo methylation and an error rate equation-based model which ignores randomness. A steady state equilibrium showing the level of sites which are methylated equals the level of sites that become demethylated with cell generation. | Does not account for randomness. Assumed an equilibrium of 80% substrate cytosine methylation for a mouse is transferrable information when analysing methylation within maize. This leads to inaccuracies of the results and differences between the model and the practical system. Did not recognize the specific roles of the DNMT’s and did not allow for the probability of sequential de novo and methylation processing. Did identify proportion of sites which become newly methylated equals the proportion of sites that become demethylated in a cell generation. |
| Capra et al (2014) | Modelling DNA methylation dynamics with approaches from phylogenetics | A continuous Markov chain model was used to combat the lack of model which take into account precursor and dependant cells. The model ascertained unobserved CpG methylation states from observations of the same sites in related cell types with a 90% accuracy rate. | Accounts for precursor to descendant relationships into and allows inference of CpG methylation dynamics. 90% accuracy rating in the inference of unobserved CpG methylation states from observed states within the related cells Model is more accurate than previous models who achieved 84% accuracy rate inferring from neighbouring CpG’s instead. Could be further optimised by integrating it within a hidden Markov chain which could clarify methylation dynamics by using genome segmentation. May not provide an improvement over existing models with regards to independent samples such as distantly related terminally differentiated cell types. |
| Sontag et al (2006) | Dynamics, stability and inheritance of somatic DNA methylation imprints. | A markov chain to show that CpG’s can alter methylation states during cell division based on conservation, de novo, loss and maintenance methylation. The model described hypomethylated to hypermethylated equilibria as a result of methylation noise in a finite system. | Markov chain inhibits the description of methylation dynamics to sample averages based on individually evolving clones and thus ignores correlations between such clones. Assumed reverse order of the two methylation processes after cell division so de novo methylation occurs before maintenance methylation. |
| Przybilla et al (2014 | Understanding epigenetic changes in ageing stem cells – a computational model approach | Further develops on the model used by Sontag et al. The model is used to understand epigenetic changes in ageing within stem cells. The findings showed that homing of stem cells niche slows down epigenetic ageing. | Model inhibits the description of methylation dynamics to sample averages based on uniquely evolving clones and therefore ignores correlations between the clones. |
| Genereux et al (2005) | A population epigenetic model to infer site-specific methylation rates from double-stranded DNA methylation patterns. | A population epigenetic probabilistic model of DNA methylation dynamics to better understand how methylated and unmethylated states of Cytosine are transferred during DNA replication. The model was designed to track methylated, hemimethylated and unmethylated CpG/CpG dyads over a number of cells from a single tissue within a single individual. The model infers site specific rates of de novo methylation and maintenance methylation, values that establish the conformity of methylation inheritance, from double stranded DNA. | Ignores the chance of mutation at the DNA sequence level that does not meet the assumption that each parent CpG gives rise to a daughter CpG on the newly synthesized complementary strand. Direct multisite information used compared to other models on the frequencies of the three dyad classes they used. Longer calculation times and detailed information needed leading to longer assay periods over other models. |
| Flottmann et al (2012) | A stochastic model of epigenetic dynamics in somatic cell reprogramming | A probabilistic Boolean model representing two kinds of stochasticity describing the interplay between gene expression, chromatin modifications and DNA methylation. The model deduced cytosine methylation rates at a number of sites within the Human promoter gene FMR1. | The Boolean model is inherently designed to overcome the uncertainty in knowledge about regulatory functions and thus massively oversimplifies the practical system which may lead to lower quality and less accurate results compared to other models. |
| Riggs and Xiong (2004) | Methylation and epigenetic fidelity | A stochastic methylation model in which for each CpG dyad there is a evident efficiency of both maintenance and de novo methylation. Methylation in most cells is dependent on site specific probabilities and is stochastically variable with regards to sites in cell lines and tissue cells. | Assumes a probability of maintenance methylation and de novo methylation associated for each CpG dyad in each DNA molecule. Model requires many iterations and an average to be taken of the results in order to gain an accurate result. |
| Jeltsch and Jurkowska (2014) | New concepts in DNA methylation | Further developed the model used by Riggs and Xiong by including the rate of cell division in conjunction with active and passive demethylation. A stochastic equation model with rates of cell division as well as rates of active and passive demethylation was used. | Assumes a probability of maintenance methylation and de novo methylation associated for each CpG dyad in each DNA molecule. Model requires many iterations and an average to be taken of the results in order to gain an accurate result. |
| Rannala et al (2001) | Methylation patterns and mathematical models reveal dynamics of stem cell turnover in the human colon | A stochastic model was utilised to analyse the methylation patterns and stem cell turnovers within the human colon The model suggested human crypts are long-lived whilst accruing random errors in methylation and consist of stem cells which undergo “bottlenecks” during life. The stochastic model simulated crypts with a methylation error rate of 2 x 10-5 per CpG site per division, with one division occurring per day. | Assumes that all CpG sites are unmethylated at birth and become methylated as cell division occurs. Rannala et al examined at least 5 different clones which provides allowing for diversity of methylation patterns to be observed within and between clones which other models do not do. |
| Haerter et al. (2014) | Collaboration between CpG sites is needed for stable somatic inheritance of DNA methylation states | A Gillespie algorithm used to implement a stochastic model of CpG islands over a number of cell cycles alongside methodical sampling of reaction parameters, producing experimental values which showed a deviation from the standard model. A dynamic collaboration was found between CpG’s can provide reliable error tolerant somatic inheritance of both hypermethylated and hypomethylated states of multiple CpGs, this reproduced witnessed, stable bimodal methylation patterns. Inheritance was predicted as being improved by the enrolment of demethylating enzymes by unmethylated CpGs, allowing CpG islands to remain hypomethylated within an expanse of hypermethylation. | Bistability of the system for inheritance of DNA methylation is the related metabolic cost. Gillespie algorithm is massively CPU intensive, must simulate many iteration. |
| Olariu et al. (2016) | Nanog, Oct4 and Tet1 interplay in establishing pluripotency. | Expanded on the work done by Haerter et al using the same stochastic model to model the regulatory network of Oct4, Tet1 and Nanog including positive feedback loops consisting of DNA demethylation over the promoters of Oct4 and Tet1. The model established that DNA methylation is the key to regulation of pluripotent genes. The model also provided a template for novel framework coupling transcription regulation with DNA methylation models. | Bistability of the system for inheritance of DNA methylation is the related metabolic cost. Provides a template for novel framework combining transcription regulation with DNA methylation models. |
| McGovern et al. (2012) | A dynamic multi-compartmental model of DNA methylation with demonstrable predictive value in haematological malignancies. | Partial differential equations were used by McGovern et al to produce a dynamic three – compartmental model of DNA methylation based on the activity of DNMT methyltransferase proteins: unmethylated CpG dyads, hemimethylated CpG dyads and methylated CpG dyads. The model also includes the Tet proteins, which enzymatically transform methycytosine to hydorxymethylcytosine. The model provided an accurate representation of the foremost epigenetic processes involving modification of DNA. | Partial differential equations used to produce this model gives it an advantage over other models being able model different scenarios such as methylation, hemimethylation and unmethylated Cpg Dyads as well as encompassing DNMT and Tet proteins which the standard models are not encompassing. |
| Zheng et al (2013) | CpGIMethPred: computational model for predicting methylation status of CpG islands in human genome | A CpGIMethPred model was used which is a support vector machine based model which forecasts the methylation status of CpG islands inside a human genome under normal conditions. The three part model system was used to gain a CpG island map. This compromised of a database extraction of methylation data, feature extraction and statistical predictive modelling. | Achieves higher specificity and accuracy than existing models by including the information about the nucleosome position, gene functions and histone acetylation whilst also maintaining proportionate sensitivity measure. |
| Lück et al (2020) | A Stochastic Automata Network Description for Spatial DNA Methylation Models | A spatial stochastic model was used to model a single CpG and generalize it into multiple CpGs using SAN (stochastic automata network) description. The results of this model were verified against extensive results from Monte Carlo simulations. | Assumes that all CpG sites are unmethylated at birth and become methylated as cell division occurs. There is however, evidence to suggest that there is somatic inheritance of methylated sites. Model is not compared to physical systems which maybe a disadvantage when analysing it’s accuracy. |
References
Åsa Johansson, S. E. (2013). Continuous Aging of the Human DNA Methylome Throughout the Human Lifespan. PLOS ONE, e67378.
Albert Jeltsch, R. Z. (2014). New concepts in DNA methylation. Trends in Biochemical Sciences, 310-318.
Andrew E. Teschendorff, U. M.-M. (2010). Age-dependent DNA methylation of genes that are suppressed in stem cells is a hallmark of cancer. Genome Research, 440-446.
Andrew P. McGovern, B. E. (2012). A dynamic multi-compartmental model of DNA methylation with demonstrable predictive value in hematological malignancies. Journal of Theoretical Biology, 14-20.
Armstrong NJ, M. K. (2017). Aging, exceptional longevity and comparisons of the Hannum and Horvath epigenetic clocks. Epigenomics, 9, 689-700.
Bjornsson HT, S. M. (2008). Intra-individual change over time in DNA methylation with familial clustering. The Journal of the American Medical Association, 299, 2877-2883.
Bocklandt S, L. W. (2011). Epigenetic predictor of age. PLOS One, 6, e14821.
Bollati V, S. J. (2009). Decline in genomic DNA methylation through aging in a cohort of elderly subjects. Mechanisms of Ageing and Development, 130, 234-239.
Casillas MA Jr, L. N. (2003). Transcriptional control of the DNA methyltransferases is altered in aging and neoplastically-transformed human fibroblasts. Molecular and Cellular Biochemistry, 252, 33-43.
Diane P. Genereux, B. E. (2005). A population-epigenetic model to infer site-specific methylation rates from double-stranded DNA methylation patterns. Proceedings of the National Academy of Sciences of the United States of America, 5802-5807.
Egerton, A. (2016). Markov Analysis – A Brief Introduction. Retrieved from egerton consulting: https://egertonconsulting.com/markov-analysis-brief-introduction/?doing_wp_cron=1587499122.9402499198913574218750
Feinberg AP, I. R. (2010). Personalized epigenomic signatures that are stable over time and covary with body mass index. Science Translational Medicine, 2, 49ra67.
Field AE, R. N. (2018). DNA Methylation Clocks in Aging: Categories, Causes, and Consequences. Molecular Cell, 882-895.
Fraga MF, B. E. (2005). Epigenetic differences arise during the lifetime of monozygotic twins. Proceedings of the National Academy of Sciences of the United States of America, 102, 10604-10609.
Issa JP, O. Y. (1994). Methylation of the oestrogen receptor CpG island links ageing and neoplasia in human colon. Nature Genetics, 7, 536-540.
Hao Zheng, H. W. (2013). CpGIMethPred: computational model for predicting methylation status of CpG islands in human genome. BMC Medical Genomics, Article number: S13.
Horvath S, a. R. (2018). DNA methylation-based biomarkers and the epigenetic clock theory of ageing. Nature Reviews Genetics 19, 371–384.
Horvath S, P. C. (2015). Decreased epigenetic age of PBMCs from Italian semi-supercentenarians and their offspring. Aging, 1159–70.
Horvath, S. (2013). DNA methylation age of human tissues and cell types. Genome Biology, R115.
J. Schaber, W. L. (2009). Nested uncertainties in biochemical models. IET Systems Biology, 1-9.
J.Catania, D. (1991). DNA methylation and cellular ageing. Mutation Research/DNAging, 283-293.
Jan O. Haerter, C. L. (2014). Collaboration between CpG sites is needed for stable somatic inheritance of DNA methylation states. Nucleic Acids Research, 2235–2244.
Jens Przybilla, T. R. (2014). Understanding epigenetic changes in aging stem cells – a computational model approach. Aging Cell, 16-18.
John A. Capra, D. K. (2014). Modeling DNA methylation dynamics with approaches from phylogenetics. BIOINFORMATICS, i408–i414.
JP, A. N. (2000). Aging, methylation and cancer. Histology & Histopathology, 835-842.
Kananen L, M. S. (2016). The trajectory of the blood DNA methylome ageing rate is largely set before adulthood: evidence from two longitudinal studies. Age, 3, Article number: 65.
Kang GH, L. S. (2003). Profile of aberrant CpG island methylation along the multistep pathway of gastric carcinogenesis. Laboratory investigation; a journal of technical methods and pathology, 83, 635-641.
Karen A. Lillycrop, S. P. (2013). DNA methylation, ageing and the influence of early life nutrition . Proceedings of the Nutrition Society, 413–421.
Katherine E. Varley, J. G. (2013). Dynamic DNA methylation across diverse human cell lines and tissues. Genome Research, 555–567.
Laura B. Sontag, M. C. (2006). Dynamics, stability and inheritance of somatic DNA methylation imprints. Journal of Theoretical Biology, 890-899.
Lisa M. McEwen, A. M. (2017). Differential DNA methylation and lymphocyte proportions in a Costa Rican high longevity region. Epigenetics & Chromatin, 10, Article number: 21.
Loukas Zagkos, M. M. (2019). Mathematical models of DNA methylation dynamics: Implications for health and ageing. Journal of Theoretical Biology, 184-193.
Maegawa, S. (2017). Caloric restriction delays age-related methylation drift. Nature Communications, 539.
Max Flöttmann, T. S. (2012). A stochastic model of epigenetic dynamics in somatic cell reprogramming. Frontiers in Physiology, Article no: 216.
Mendelsohn, L. (2017). Epigenetic Drift Is a Determinant of Mammalian Lifespan. Rejuvenation Research, 430-436.
Pappas, S. (2018, January 30). Weird: Naked Mole Rats Don’t Die of Old Age. Retrieved from Live Science: https://www.livescience.com/61568-naked-mole-rats-no-aging.html
Peter D. Fransquet, J. W. (2019). The epigenetic clock as a predictor of disease and mortality risk: a systematic review and meta-analysis. Clinical Epigenetics, 11:62.
Rannala, S. R. (2001). Methylation patterns and mathematical models reveal dynamics of stem cell turnover in the human colon. Proceedings of the National Academy of Sciences of the United States of America, 10519-10521.
S. Bouwman, G. B. (2005). ADVANTAGES OF PROBABILISTIC SYSTEM ANALYSIS. INTERNATIONAL CONFERENCE ON ELECTRICITY DISTRIBUTION, CIRED 2005.
Sarah P. Otto, V. W. (1990). DNA Methylation in Eukaryotes: Kinetics of Demethylation and de Novo Methylation During the Life Cycle. Genetics Society of America, 429-437.
Sauer, M. H. (2010). Systems biology of microbial metabolism. Current Opinion in Microbiology, 337-343.
Scitable. (2014). population bottleneck. Retrieved from Nature.com: https://www.nature.com/scitable/definition/population-bottleneck-300/
Scitable. (2019). species. Retrieved from Nature.com: https://www.nature.com/scitable/definition/species-312/
Singhal RP, M.-H. L. (1987). DNA methylation in aging of mice. Mechanisms of Ageing and Development, 41, 199–210.
Soni, D. (2018). Introduction to Markov Chains. Retrieved from towards data science: https://towardsdatascience.com/introduction-to-markov-chains-50da3645a50d
Sonia Shah, A. F. (2014). Genetic and environmental exposures constrain epigenetic drift over the human life course. Genome Research, 1725-1733.
Southern, J. P.-F.-F. (2008). Multi-scale computational modelling in biology and physiology. Progress in Biophysics and Molecular Biology, 96, 60-89.
Stephanie. (2016). Stochastic Model / Process: Definition and Examples. Retrieved from Statistics How To: https://www.statisticshowto.com/stochastic-model/
Stephanie. (2017). Probabilistic: Definition, Models and Theory Explained. Retrieved from statistics how to: https://www.statisticshowto.com/probabilistic/
Sun, D. (2014). Epigenomic Profiling of Young and Aged HSCs Reveals Concerted Changes during Aging that Reinforce Self-Renewal. Cell Stem Cell, 673-688.
Talens RP, B. D. (2010). 45. Talens RP, Boomsma DI, Tobi EW et al. (2010) Variation, patterns, and temporal stability of DNA methylation: considerations for epigenetic epidemiology. The FASEB Journal, 24, 3135-3144.
Victor Olariu, C. L. (2016). Nanog, Oct4 and Tet1 interplay in establishing pluripotency. Scientific Reports , Article number: 25438.
Wolf, A. L. (2020). A Stochastic Automata Network Description for Spatial DNA-Methylation Models . International Conference on Measurement, Modelling and Evaluation of Computing Systems, 54-64.
Xiong, A. D. (2004). Methylation and epigenetic fidelity. Proceedings of the National Academy of Sciences of the United States of America, 4-5.

Hassan graduated with a Master’s degree in Chemical Engineering from the University of Chester (UK). He currently works as a design engineering consultant for one of the largest engineering firms in the world along with being an associate member of the Institute of Chemical Engineers (IChemE).