We will be looking at energy balances on reactors, first two terms need to be understood these are, isothermal which refers to a system at a constant temperature, adiabatic involves no heat entering or leaving the system and open system which refers to mass being able to enter and leave the system and can be lost to or gained from the surrounding, knowing and understanding these terms will help in this section.
What Is An Energy Balance?
Energy balance is simply the difference in the energy input and output and an energy balance equation can be used on open systems and can be relatively easy to do or challenging when more components and different phases are present.

Figure 1. Energy balance diagram for an open system
The Energy Balance Equation For Open Systems:

(1.11)
The energy balance equation flow reactors in open systems (1.11), which is valid for non-isothermal reactors that have no phase change, and a reference species A has been used:

Where:

The enthalpy of reaction at a certain temperature (T) is worked out using the enthalpy of products and reactants
Example:
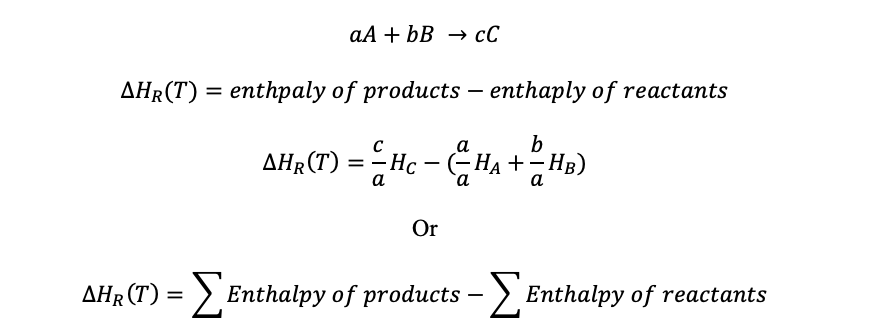

Hassan graduated with a Master’s degree in Chemical Engineering from the University of Chester (UK). He currently works as a design engineering consultant for one of the largest engineering firms in the world along with being an associate member of the Institute of Chemical Engineers (IChemE).


