Suggestions

Suggestions

Batch And Levenspiel Plots For Parallel And Series Reactors

August 28, 2020
by
Navigate This Article show

Batch and Levenspiel Plots

A Batch reactor plot is a graphical representation of the volume of an isothermal system.

General shape of a Batch Reactor (Advanced Energy Materials Processing Laboratory, 2020)

Batch reactor plot (Advanced Energy Materials Processing Laboratory, 2020)

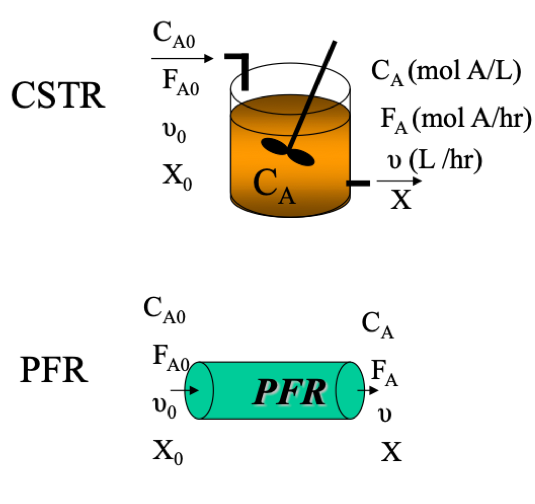
A Levenspiel plot is a representation of the continuous flow reactor; CSTR and PFR design equations as a function of conversion and is used to determine the volume of the reactor.

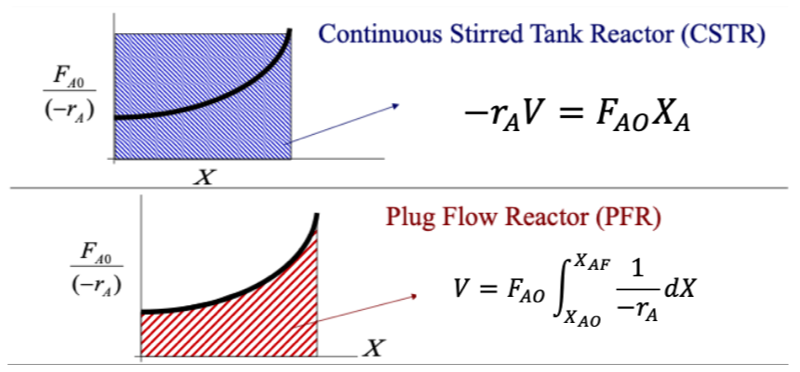
Shape of CSTR and PFR (Advanced Energy Materials Processing Laboratory, 2020)

PFR and CSTR Levenspiel Plot Comparison

The rate used for the CSTR is evaluated at the exit stream conditions while for the PFR the rate used is integrated over a range of conditions and we can solve this using Simpsons composite rule,

CSTR and PFR Levenspiel plot (Advanced Energy Materials Processing Laboratory, 2020)

  • PFR requires a smaller volume than the CSTR for a given conversion
  • When the reaction speed increases for a CSTR the Levenspiel plot will curve downwards as the conversion changes and will require a smaller CSTR volume.

Levenspiel Plot For Reactor In A Series Arrangement

PFR in series act as one large PFR and if the density is constant then the residence time is just the space time at the inlet conditions. For a CSTR multiple CSTRs in series require a smaller volume as a CSTR is evaluated at the output conditions and will make a series of CSTR’s smaller than one large CSTR, as when using multiple CSTRs the first tank operates at a lower conversion so the concentration of reactants will be higher so the rate will be greater and the volume required will be smaller.

CSTRs in series get close to the performance of PFR and the smaller the CSTRs the closer they get, but financial costs and available space and other factors make having lots of small CSTRs not practical when one PFR can be used.

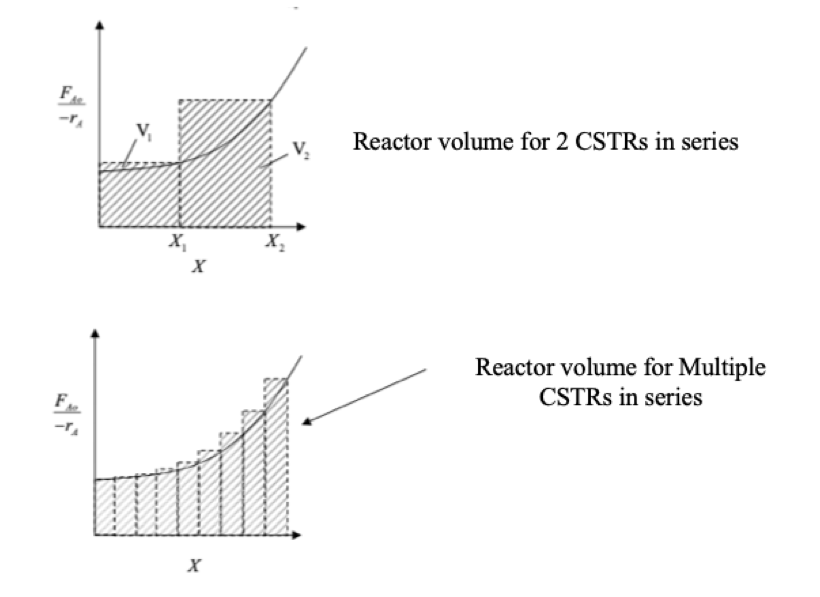
CSTR Levenspiel plot in series (MIT, 2007)

Parallel Reactors

Parallel reactors for equal-sized flow reactors, the feed stream is split evenly between the reactors. Parallel reactor arrangement is used for CSTRs as the reactors will be operating at the lowest conversion will be better to operate in series. For PFRs this arrangement behaves as one large PFR and is a common arrangement as used in industry or in Labourites.

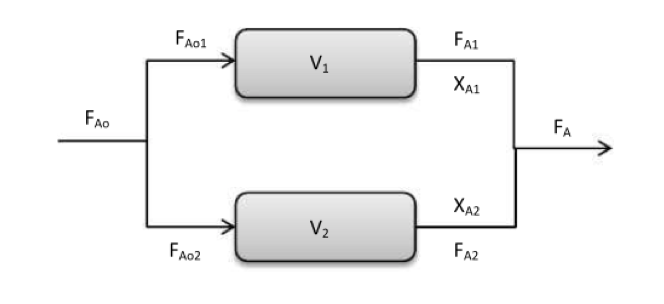
PFR in a parallel arrangement (Santofimio, 2020)

PFR With Recycle

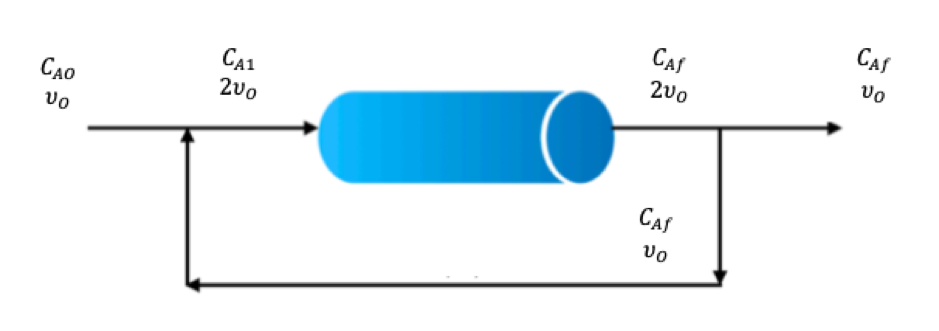
Unreacted reactants can be recycled from the PFR exit stream, we define a recycle ratio, R when it is equal to zero (R = 0) then we have standard/normal plug flow and as R increases we develop mixed flow and the PFR starts to resemble the behaviour of a CSTR.

R = Volume of fluid recycledVolume of fluid leaving PFR

(1.11)

We will be adding two new terms, single-pass conversion XS and overall conversion XO, the equations are below and have used species ‘A’ to represent the species used.

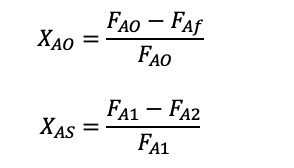
Single-pass conversion shows the fraction that is converted when it goes through the PFR once and overall conversion is the fraction converted in the final stream from the total inlet flow.

PFR with recycle diagram (Cheggstudy, 2020)

PFR with recycle is a difficult concept to get your head around and has a lot of keywords, that can trip you up if you don’t pay attention them, the best way is to do an example whilst looking at the answers and see what steps to do to solve this type of question in an exam, if you can do this example exam question without looking at the answers it will be extremely impressive!

Example – PFR with recycle (typical exam question)

In a PFR with recycle a reaction that is elementary and, in the liquid phase takes places, with an R = 1 and a conversion of 2/3, what is the conversion if there is no recycle stream?

Answer – PFR with recycle

First: do PFR with recycle stream

As liquid phase reaction only, the density is constant so the volumetric flow rate is constant, we will use the PFR mole balance but will use a slightly different version, this will help as there are different conversions and can be tricky to do.

Mole Balance PFR:

∆FA = rA∆V

Rate Equation:

-rA = kCA2

From Stoichiometry:

FA = vCA

Draw the diagram as seen above with the information we already have; this will help you visualise the problem:

The volumetric flow rate (v) is initially:

v0

and as the recycle ratio is one the volumetric flow rate in the recycle is same as feed stream, thus the stream going into the reactor after the recycle would be:

v0 + v0 = 2v0

The final concentration is:

CAf = CA03

as the conversion is 2/3, this is from the overall conversion.

The concentration in the feed stream is:

CA1 = (CA0 + CAf) × 12 = 2CA03

this is because the volumetric flow rates are equal in the recycle stream and the feed stream. We multiply by a ½ as the recycle stream and feed are equal so assume perfect mixing.

Now take the PFR mole balance and the stoichiometric relationship to get:

v∆CA = rA∆V

And as volumetric flow rate into the reactor is:

v = 2v0

we therefore get:

2v0∆CA = rA∆V

This can be rearranged to:

∆CArA=∆V2v0

Then substitute in the rate law:

∆CA-KCA2=∆V2v0

Now integrate to get:

∫CA1CAf1KCA = V2v0

1KCAf – 1KCA1 = V2v0

We already know the values of the concentrations, so the left-hand side of the equation becomes:

1KCAf3-1K2CA13 = 32KCA0

32KCA0= V2v0or KVCA0v0 = 3

This above relationship will be true whether the recycle stream is on or not!

Second: do PFR without recycle stream:

Mole balance PFR:

∆FA = rA∆V

As no recycle the volumetric flow rate entering the reactor is:

v0

Thus, combining stoichiometry and mole balance:

v0∆CA=rA∆V

Now substitute in rate equation and integrate:

∫CA1C*Af1KCA = Vv0

We have put an * on CAf as this value will be different when the recycle stream is on.

1C*Af-1CA1 =KVv0

CA0C*Af-1 = CA0KVv0 = 3

Therefore:

CA0C*Af = 4

So, the exit concentration (C*Af ) without recycle is ¼ of the feed concentration.

Conversion without Recycle:

X0 = 1-14 = 34

Conversion with Recycle: 2/3

References

Advanced Energy Materilas Processing Laboratory. (2020). CHE 309: Chemical Reaction Engineering. Retrieved from Advanced Energy Materilas Processing Laboratory: http://aempl.kist.re.kr/wp-content/files/Lecture-5_Ch2.pdf

Cheggstudy. (2020). Question: Problem 3: Recycle Reactor. Retrieved from Cheggstudy: https://www.chegg.com/homework-help/questions-and-answers/problem-3-recycle-reactor-farmer-michael-process-setting-recycle-reactor-farm-reaction-tak-q26913611

MIT. (2007). PFR vs. CSTR: Size and Selectivity. Retrieved from MIT: https://ocw.mit.edu/courses/chemical-engineering/10-37-chemical-and-biological-reaction-engineering-spring-2007/lecture-notes/lec09_03072007_w.pdf

Santofimio, D. S. (2020). Parallel Reactors.docx. Retrieved from Scribd: https://www.scribd.com/document/242835751/Parallel-Reactors-docx

Leave your vote

1 Point
Upvote Downvote
Previous Story

An In Depth Guide To Basic Reaction Kinetics

Next Story

An In-Depth Breakdown | PFR and CSTR Reactor Design

Log In

Forgot password?

Forgot password?

Enter your account data and we will send you a link to reset your password.

Your password reset link appears to be invalid or expired.

Log in

Privacy Policy

Add to Collection

No Collections

Here you'll find all collections you've created before.

Privacy Preference Center

Privacy Preferences